Big O Notation
What is code performance?
- It is measured along resource consumption and the code consumes a variety of resources
- Improving code performance beyond a certain point involves tradeoffs
- Performance is all about trade-offs
How to measure performance?
- Time: How long it will take to run?
- Space:How much memory or disk space program occupy? how much extra space is needed
- Network: How much data transfer over the network
- Efficient code uses fewer resources along all these axes
- Code can be more performant when it uses the resources we have in plenty rather than those we lack
- If you have more memory and disk space you can cut down the processing time of your code
- As a developer we need to understand it is a time critical system or space critical system
Time
- The amount of processing
- Number of operations code has to perform to accomplish it's objective
- Operation takes time
Space
- Memory needed by code to store information at runtime and disk space
- Code need persistent storage
Network
- The bandwidth code uses to pass information to client or other machine
What is complexity?
- It measure of how resources requirements change as the size of the problem gets larger
- Complexity depends on the size of the input
- Any program can run fast, but when the input is larger such as millions of elements then complexity of code is important
- Complexity affects performance.More complex code means lower the performance
- As size of the input grows how much worse is the procession time.
- Always compare worst case
Complexity and the Big -O notation
- What is the complexity of this code?
- How would you measure this code using Big O notation?
- Code complexity
- Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity
What is Big O?
- The Big O notation is an approach for analyzing the performance of an algorithm
- Code comparing
- Comparing worst case
- This express the complexity of an algorithm
- Big O cheat Sheet
O(1) Constant time complexity
- An algorithm whose complexity does not change with the input size is O(1) or order of (1)
- O(1) is said to have a constant time complexity
- No matter what is the input size it run on constant
- if it took 10 seconds to run will always take 10 seconds no matter the input size is in millions
- O(1) is the fast algorithm

Complexity
| Method | Time Complexity | Reason |
|---|---|---|
sum() | O(1) | Simple arithmetic + return |
array() | O(n) | Because of loop through array |
| Array index | O(1) | Direct access by index |
constant() | O(1) | Single assignment |
O(1) code demo
Github code sample O(1)
O(n) Linear/Proportional time complexity
- The complexity of an algorithm is O(n) if the time taken by the algorithm increases linearly when N increases
- For e.g N =100 and it takes 100 seconds to process those elements
- Now increase the input by N= 200 it will take 200 seconds to process
- Algorithm is said to be O(N) as N increases by the time
String[] names = {"Alex", "Brian", "Cathy", ..., "Zoe"};
for (String name : names) {
System.out.println(name); // Print each name
}
If the list has 100 names, we print 100 lines.
✅ If it has 1,000 names, we print 1,000 lines.
That’s O(n) behavior.
O(n) code demo
Github code sample O(n)
O(n2) Quadratic time complexity
- The complexity of an algorithm is O(n2) if the time taken by the algorithm increases quadratically
- For e.g N becomes 2N and it will double
- Now increase the input by N= 100 it will take 200 seconds to process
- The time taken increased quadratically based on input size
- Loop within a loop
- It will take 100 steps to sort 10 items, 10000 steps to sort 100 items, 1,000,000 steps to sort 1000 items.
- Algorithm degrades quickly.
O(n2) code demo
Github code sample O(n2)
O(log n)Logarithmic time complexity
- When the size of the input data decreases in each step by a certain factor, an algorithm will have logarithmic time complexity.
- This means as the input size grows, the number of operations that need to be executed grows comparatively much slower.
- Divide and Conquer If the input size is huge but you're halving it each time → the algorithm is O(log n).
- e.g Binary Search log 2 8=3
- 2 ? =8
- log₂(8) = 3 (because 2³ = 8)
- log2 1073741824 =31 O( log n)


Big O complexity
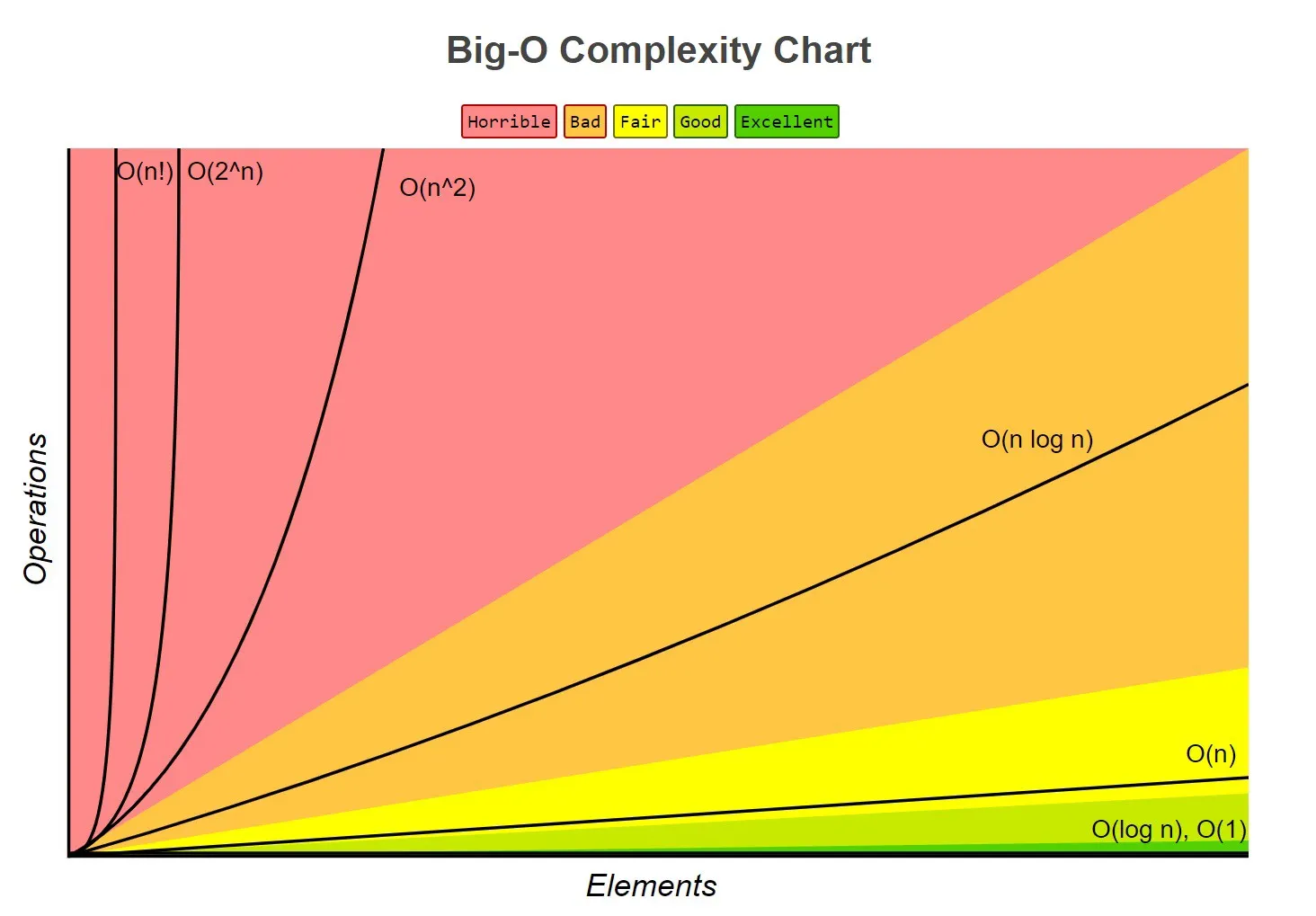
Binary Search
O(n2) code demo
Github code sample O(n2)
Which algorithms are faster?
- O(1)< O(n) < O(n2) < O(n3.....)
- source https://www.freecodecamp.org/
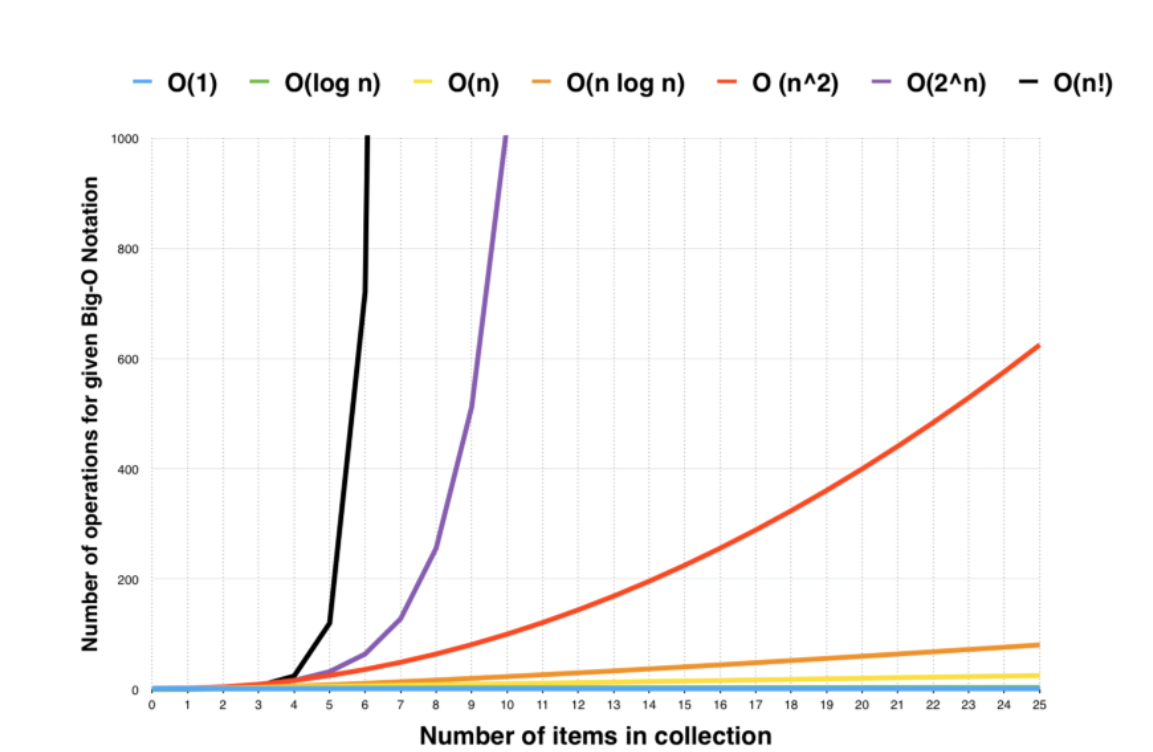
Which algorithms are faster?
| Data Structures | Space Complexity | Average Case Time Complexity | |||
| Access | Search | Insertion | Deletion | ||
| Array | O(n) | O(1) | O(n) | O(n) | O(n) |
| Stack | O(n) | O(n) | O(n) | O(1) | O(1) |
| Queue | O(n) | O(n) | O(n) | O(1) | O(1) |
| Singly Linked List | O(n) | O(n) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(n) | O(n) | O(1) | O(1) |
| Hash Table | O(n) | N/A | O(1) | O(1) | O(1) |
| Binary Search Tree | O(n) | O(log n) | O(log n) | O(log n) | O(log n) |
Linked Lists complexity
- List data structures they can store multiple elements as a list
- Each element is linked to or reference the next element. It is chained together
- Adding a new element to the beginning of a list O(1)
- Deleting a first element to the beginning of a list O(1)
- Adding a new element to the end of a list O(N)
- Finding an element in a linked list O(N)
- Deleting a random element in a linked list O(N)
- Linked List complexity
| Operation | What it Means | Time (Big O) | Why |
|---|---|---|---|
| ➕ Add at the beginning | Add a new item at the front | O(1) | Just link the new item to the head of the list — super fast! |
| ❌ Delete the first item | Remove the first node | O(1) | Just move the "head" pointer to the next node |
| ➕ Add at the end | Add an item at the end | O(n) | You need to go through the whole list to find the end first |
| 🔍 Find an item | Search for something | O(n) | You might have to check every node until you find it |
| ❌ Delete random item | Remove an item from the middle | O(n) | First you have to search for it, then remove it |
Stack complexity (LIFO)
- A stack is like a stack of plates — you can only add or remove the top plate. It's based on the rule Last In, First Out (LIFO).
- Implementation of undo in an application
- Implementing the back button on the web browser
- Push and Pop from a stack is O(1) constant time complexity
- isempty() and isFull() also O(1) constant time complexity
- The use of "size()" variable makes getting the size of the stack also O(1)
- Space complexity is O(n)
- Stack complexity
| Operation | What it Means | Time (Big O) | Why |
|---|---|---|---|
push() | Add an item on top | O(1) | It goes directly to the top — no searching needed |
pop() | Remove the top item | O(1) | Just remove the item on top |
isEmpty() / isFull() | Check if stack is empty or full | O(1) | Just a quick check — no need to go through items |
size() | Get number of items | O(1) | If you keep a counter variable, it’s instant |
Queue complexity (FIFO)
- A queue is like a real-life line (like waiting in line for ice cream 🍦):
- First In, First Out (FIFO) – the first person to get in line is the first one to be served.
- enqueuing and dequeuing from a queue is O(1) constant time complexity
- Space complexity is O(n)
- isempty() and isFull() also O(1) constant time complexity
- Circular queue works best for the queue underlying data structure
- Queue complexity
| Operation | What It Means | Time (Big O) | Why |
|---|---|---|---|
enqueue() | Add an item to the back of the queue | O(1) | Just place it at the end — no searching needed |
dequeue() | Remove an item from the front | O(1) | Always remove the first item |
isEmpty() / isFull() | Check if the queue is empty or full | O(1) | Quick check — no scanning required |
| Space Used | Memory needed for all items | O(n) | Because it holds n items |
Selection Sort complexity
- Selection Sort is like organizing playing cards by always picking the smallest one and placing it in the right spot.
- At each iteration 1 element is selected and compared with every other element in the list to find the smallest one
- First we find the smallest element, get it into the first position and next we find the second smallest till the entire list is sorted
- comparison N-1
- The complexity of selection sort is O(n2)
Bubble Sort complexity
- For each iteration every element is compared with its neighbor and swapped if they are not in order.
- The result in smaller elements bubble to the beginning of the list
- The complexity of Bubble sort is O(n2)
Insertion Sort complexity
- Start with a sorted sub-list of size 1
- Insertion sort the next element into the sorted sub-list at the right position. Now the sorted sub list has 2 elements
- This continues till the entire list is sorted
- The complexity of Insertion sort is O(n2)
- This is similar to bubble sort it is adaptive in that nearly sorted lists complete very quickly
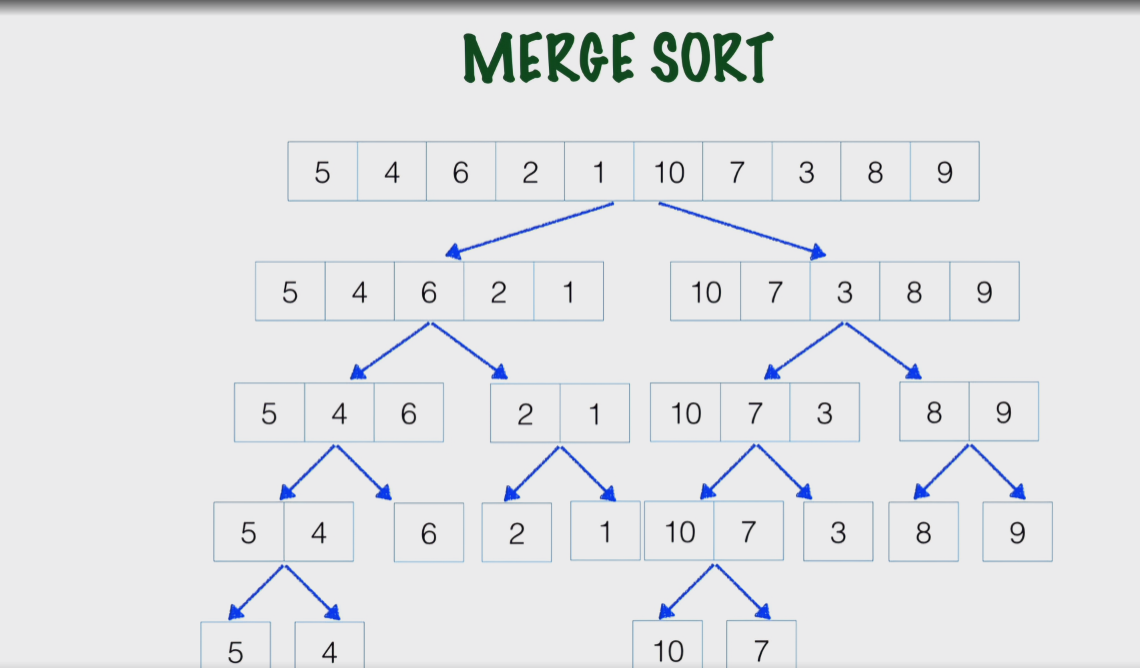
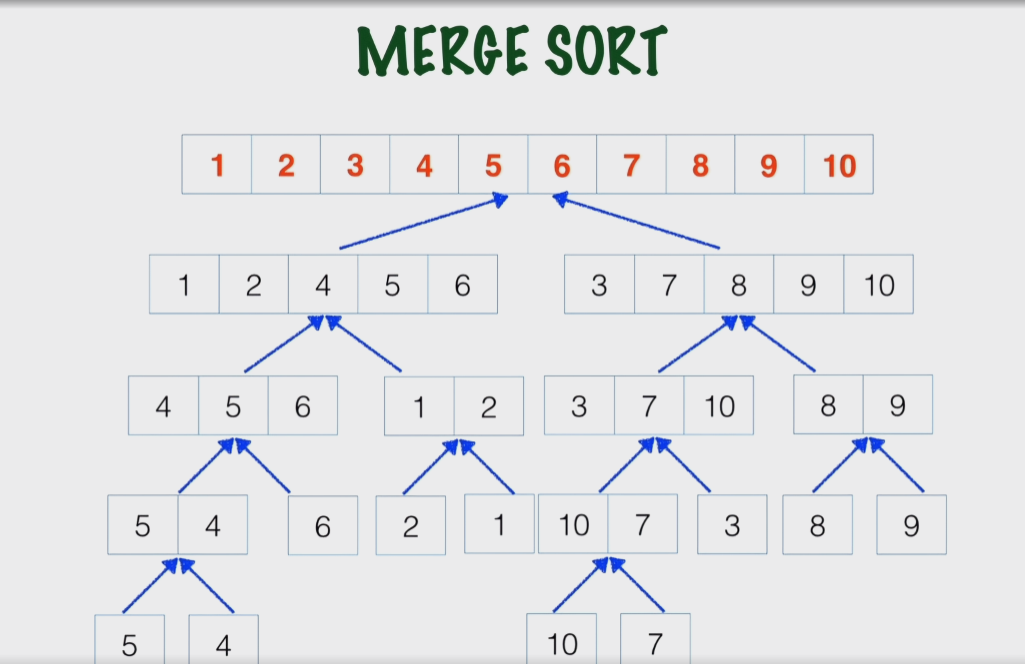
Merge Sort complexity
- Use Divide and conquer approach
- Use recursion
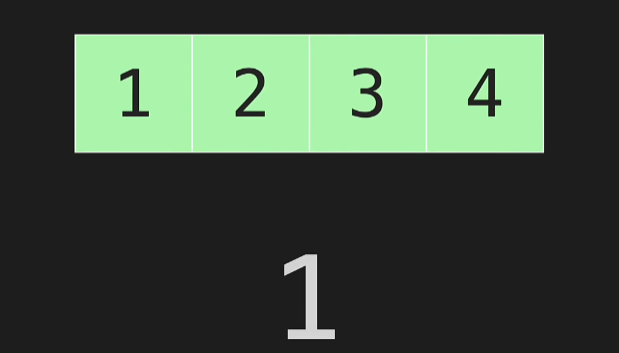
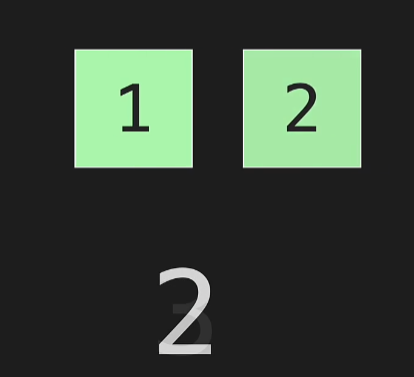
- At some point there will be a list of length one
- The complexity of Merge sort is O(n Log(n))
- Splitting the list takes log(n) steps (because you cut it in half each time).
- Merging takes n steps total (you look at every item once when combining).
Splitting (log n) × Work per level (n) = O(n log n)