Sorting & Searching
Sorting
- Sorting: Rearranging the values in an array or collection into a specific order (usually into their "natural ordering").
- Sorting is a classic subject in computer science
- Sorting algorithms illustrate many creative approaches to problem solving, and these approaches can be applied to solve other problems
- Sorting algorithms are good for programming fundamental using selection statements, loops, methods and arrays.
- Sorting algorithms are excellent examples to demonstrate algorithm performance
Sorting
Sorting
- Can be solved in many ways:
- There are many sorting algorithms
- Some are faster/slower than others
- Some use more/less memory than others
- Some work better with specific kinds of data
- Some can utilize multiple computers / processors
Insertion Sort
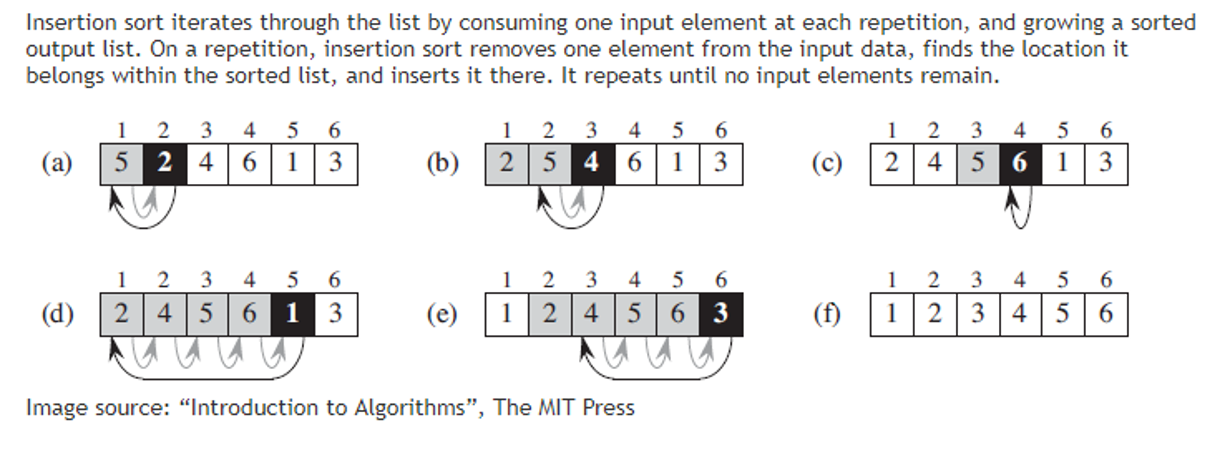
- Sorts a list of values by repeatedly inserting a new element into a sorted sub list until the whole list is sorted.
- Sorted – all items to the left are smaller
- The complexity of the insertion sort algorithm is Θ(n^2).
- Worst case time complexity: Θ(n^2) n is the size of the array
- Average case time complexity: Θ(n^2)
- Best case time complexity: Θ(1) sorted array
How Insertion Sort Works?
Insertion Sort Code
Github code sample Insertion Sort
Insertion Sort
Bubble Sort
- Bubble sort, also referred to as sinking sort
- Works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items and swapping them if they are in the wrong order
- It only uses comparisons to operate on elements, it is a comparison sort
- Bubble sort has worst-case and average complexity both Θ(n^2), where n is the number of items being sorted
- Insertion sort, tend to have better performance than bubble sort. Therefore, bubble sort is not a practical sorting algorithm when n is large. Performance of bubble sort over an already-sorted list (best-case) is O(n).
Bubble Sort
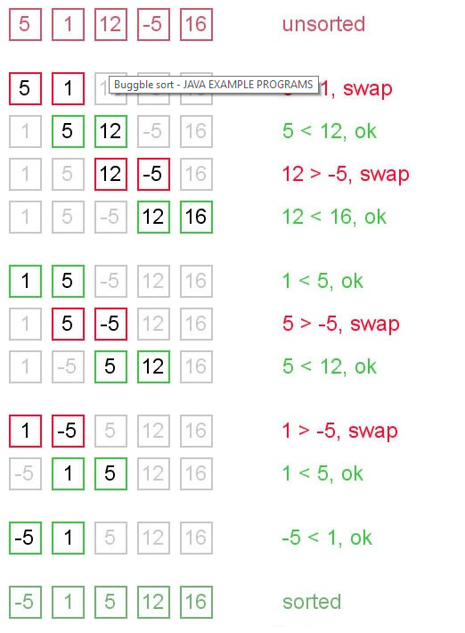
How Bubble Sort Works?
Bubble Sort Code
Github code sample Bubble Sort
Merge Sort
- Merge sort is a neat algorithm, because it’s “the sort that sorts itself”.
- Merge sort is a divide and conquer algorithm.
- This means that merge sort requires very few comparisons and swaps
- Divide the unsorted array into n partitions, each partition contains 1 element. Here the one element is considered as sorted.
- Repeatedly merge partitioned units to produce new sub list until there is only 1 sub list remaining. This will be the sorted list at the end.
Merge Sort
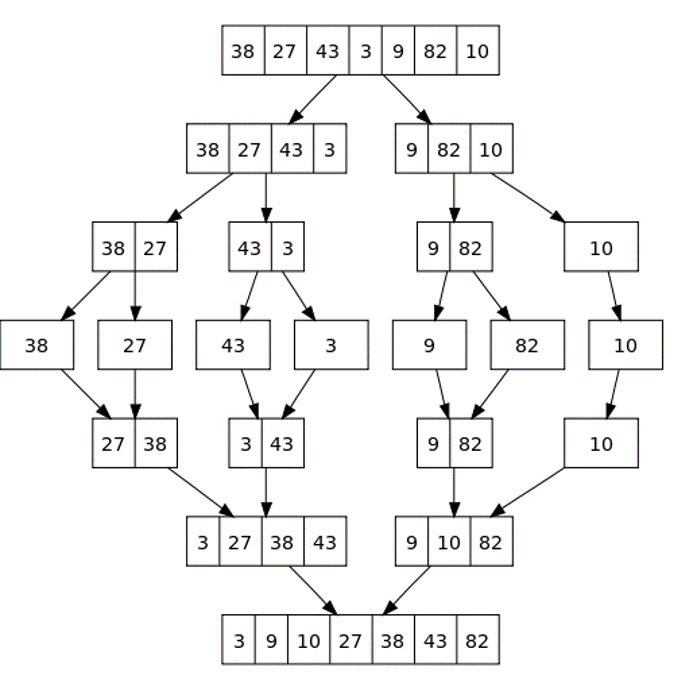
How Merge Sort Works?
Merge Sort Code
Github code sample Merge Sort
Quick Sort
- Quicksort or partition-exchange sort, is a fast sorting algorithm, which is using divide and conquer algorithm.
- Quicksort first divides a large list into two smaller sub-lists: the low elements and the high elements. Quicksort can then recursively sort the sub-lists
- The complexity of quick sort in the average case is Θ(n log(n)) and in the worst case is Θ(n^2).
Quick Sort
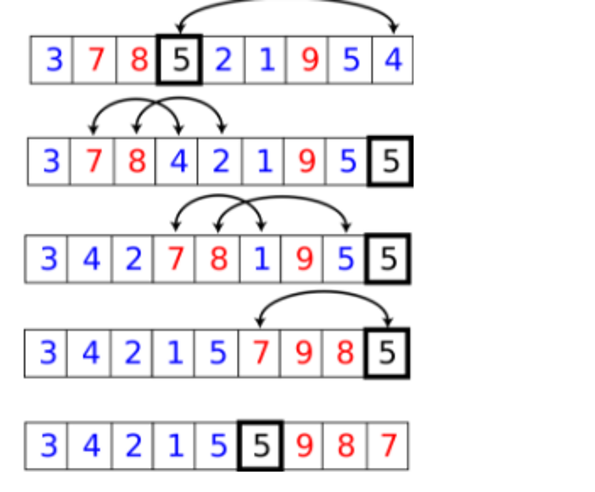
How Quick Sort Works?
Quick Sort Code
Github code sample Quick Sort
Heap Sort
- A heap is a tree with some special properties, so value of node should be greater than or equal to(less than or equal to in case of min heap) children of the node and tree should be complete binary tree.
- Binary heaps are those heaps which can have up to 2 children.
Heap Sort
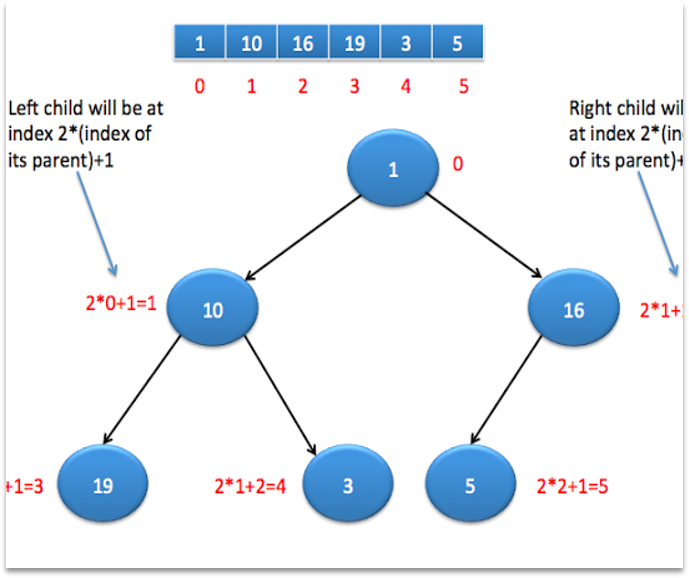
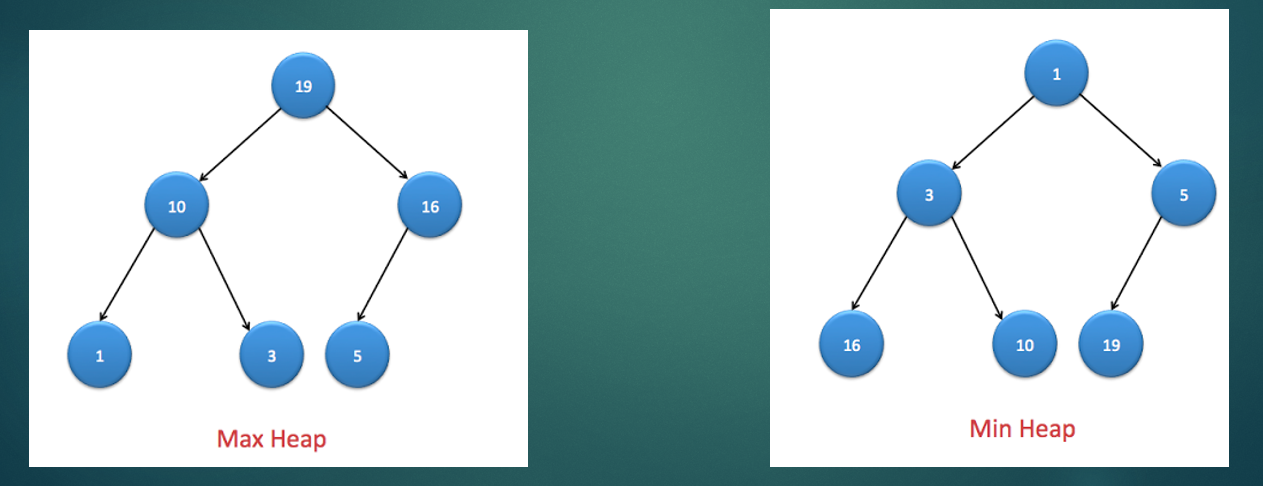
Types of Heaps
- Max Heap: It is binary heap where value of node is greater than left and right child of the node.
- Min Heap: It is binary heap where value of node is lesser than left and right child of the node.
How Heap Sort Works?
Heap Sort Code
Github code sample Heap Sort
Bucket Sort
- Bucket Sort is a sorting algorithm in which elements of given array are distributed into different buckets and then each bucket is sorted individually using some other sorting technique or recursively using bucket sort.
Bucket Sort

How Bucket Sort Works?
Bucket Sort Code
Github code sample Bucket Sort
Selection Sort
- In selection sort algorithm, we search for the lowest element and arrange it to the proper location.
- We swap the current element with the next lowest number
Selection Sort

How Selection Sort Works?
Selection Sort Code
Github code sample Selection Sort
Some other sorting algorithms
- Bogo Sort,Bubble Sort,Bucket Sort,Cocktail Sort,Counting Sort,Cycle Sort,Exchange Sort,Fisher Yates Shuffle,Pancake Sort,Parallel Sort,Quick Sort,Shell Sort,Sorting An Array Of Objects,Sorting Using A Stack,Sorting an ArrayList
Searching Algorithms
- The fundamental problem in searching is to retrieve the record associated with a given search key in order that the information in the record be made available for processing.
Linear Search
- A linear search scans one item at a time, without jumping to any item .
- The worst case complexity is O(n), sometimes known an O(n) search
- Time taken to search elements keep increasing as the number of elements are increased.
Linear Search
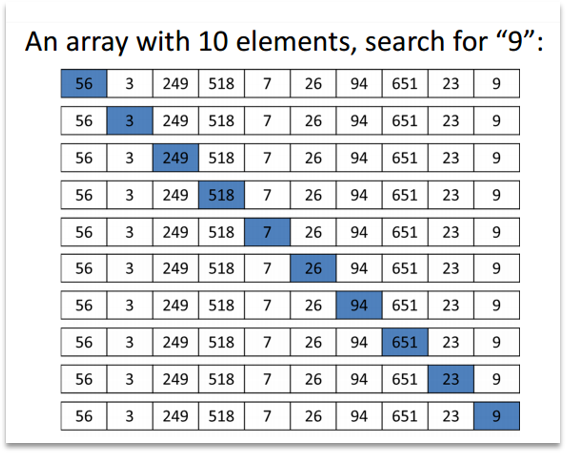
How Linear Search Works?
Linear Search Code
Github code sample Linear Search
Binary Search
- Search a sorted array by repeatedly dividing the search interval in half.
- Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half.
- Otherwise narrow it to the upper half. Repeatedly check until the value is found, or the interval is empty.
Binary Search
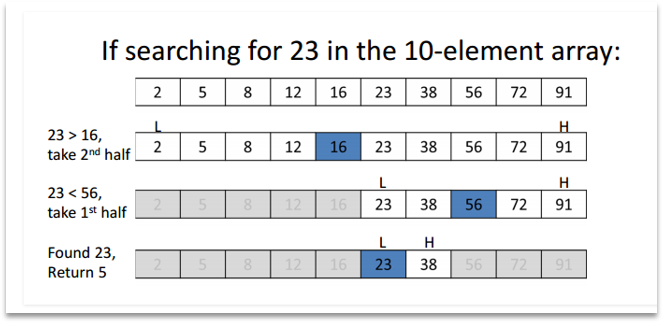
How Binary Search Works?
Binary Search Code
Github code sample Binary Search